Inverse Quantum Fourier Transform in Qiskit v2.x
In the previous article, we explored concrete examples and advantages of the Quantum Fourier Transform.
In this article, we will implement the Inverse Quantum Fourier Transform using Qiskit v2.x and verify that the original quantum state can be correctly identified.
IBM Certified Quantum Computation Practice Exams
Practice exams aligned with the latest exam version, “IBM Certified Quantum Computation using Qiskit v2.X Developer – Associate,” have been released. Use this practice exam collection to boost your score and increase your chances of passing.
Amazon Braket Learning Course
You can efficiently learn the basic knowledge of quantum computing-including quantum gates and quantum circuits as well as how to use Amazon Braket through this course.
This course is designed for those with no prior knowledge of quantum computing or AWS, and by the end, you’ll even be able to learn about quantum machine learning. Take advantage of this opportunity to build your skills in quantum technologies!
Inverse Quantum Fourier Transform in Qiskit 2.0
In the previous article, we explained that if a 2-qubit quantum state existed in either state $\psi_1 = \frac{1}{2} \left( \ket{00} + i\ket{01} - \ket{10} - i\ket{11} \right)$ or $\psi_2 = \frac{1}{2} \left( \ket{00} - \ket{01} + \ket{10} - \ket{11} \right)$, it is possible to determine which state it is by applying the Inverse Quantum Fourier Transform.
In this article, we will perform the Inverse Quantum Fourier Transform using Qiskit and verify that the original quantum state can be correctly identified.
Firstly, let’s import the necessary functions.
from qiskit import QuantumCircuit
from qiskit.circuit.library import StatePreparation
from qiskit.primitives import StatevectorSampler
from qiskit.circuit.library import QFT
We define Sampler and Quancum Cruicuit.
sampler = StatevectorSampler()
n_qubits = 2
qc = QuantumCircuit(n_qubits, 2)
In this article, we set the target quantum state to $\psi_2$, and append the quantum circuit that generates this state below.
state = [1/2, - 1/2, 1/2, - 1/2]
prep = StatePreparation(state)
qc.append(prep, [0, 1])
By simply measuring the quantum state at this point, we can only obtain results like the ones below, and it is not possible to determine whether the state was $\psi_1$ or $\psi_2$.
qc.measure([0,1], [0,1])
pub = (qc, None)
job = sampler.run([pub], shots=100)
result=job.result()[0]
print(result.data.c.get_counts())
# Output
{'01': 27, '10': 27, '11': 23, '00': 23}
Let’s implement the Inverse Quantum Fourier Transform.
iqft = QFT(num_qubits=n_qubits, inverse=True, do_swaps=True)
qc.append(iqft, [0, 1])
qc.measure([0,1], [0,1])
The overall circuit is as follows.
As explained in the previous article, if $\ket{01}$ is observed, we know that the original state was $\psi_1$, while if $\ket{10}$ is observed, we know that it was $\psi_2$.
qc.draw('mpl')
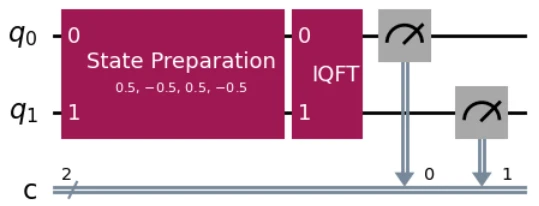
Let’s execute the quantum circuit.
pub = (qc, None)
job = sampler.run([pub], shots=100)
result=job.result()[0]
print(result.data.c.get_counts())
As shown below, the result observes state $\ket{10}$, indicating that state $\psi_2$ was originally generated. Similarly, if you generate state $\psi_1$ and then apply the Inverse Quantum Fourier Transform, you will observe state$\ket{01}$. Give it a try when you have a moment.
# Output
{'10': 100}
In the next article, we will use Amazon Braket SDK to implement the inverse Quantum Fourier Transform.
IBM Certified Quantum Computation Practice Exams
Practice exams aligned with the latest exam version, “IBM Certified Quantum Computation using Qiskit v2.X Developer – Associate,” have been released. Use this practice exam collection to boost your score and increase your chances of passing.
Amazon Braket Learning Course
You can efficiently learn the basic knowledge of quantum computing-including quantum gates and quantum circuits as well as how to use Amazon Braket through this course.
This course is designed for those with no prior knowledge of quantum computing or AWS, and by the end, you’ll even be able to learn about quantum machine learning. Take advantage of this opportunity to build your skills in quantum technologies!