Qiskit 2.0で量子位相推定(Quantum Phase Estimation)
これまでの記事では以下の内容を学びました:
今回はQiskit 2.0を用いて、量子位相推定を実行します。
Amazon Braket学習コース
この記事で登場する、量子ゲートや量子回路など、量子コンピュータの基本的な知識や、Amazon Braketの使い方についてはこちらのコースで効率的に学べます。
量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう!
はじめての量子コンピューター入門【基礎知識・Qiskitでの実装・量子機械学習 全て学べる】
量子コンピューターの入門コースを作成しました。このコースにより、量子コンピューターの基礎知識、Qiskitでの実装、量子機械学習について学べます。
Qiskit 2.0で量子位相推定
今回は対象のユニタリ行列を$S$ゲート、固有状態を$\ket{1}$として実装してみましょう。 つまり量子位相推定により$\ket{1}$に対する$S$ゲートの固有値を求めます。暗算でもこの固有値の結果は算出できるかもしれませんが、あえて分からないふりをして進めていきましょう。 まずは必要となる関数をimportします。
from qiskit import QuantumCircuit
from qiskit.primitives import StatevectorSampler
from qiskit.circuit.library import QFT
from qiskit.circuit.library import SGate
samplerを定義します。
sampler = StatevectorSampler()
量子回路を定義します。今回読み出しレジスタの量子ビット数は3とします。
n_qubits = 4
n_readout_qubits = n_qubits - 1
qc = QuantumCircuit(n_qubits, n_readout_qubits)
読み出しレジスタの量子ビットにはHゲートを書けるのでした。
for qubit in list(range(n_readout_qubits)):
qc.h(qubit)
また、末尾のビットとなる4量子ビット目は固有状態$\ket{1}$に変換しておきます。
qc.x(n_readout_qubits)
続いて制御$S$ゲートを適用します。前回での記事での説明の通り、量子ビットに依存して$2^{n-1}$回だけ制御$S$ゲートを適用しなければいけないことに注意しましょう。
ctrl_s = SGate().control(1)
for ctl_bit in list(range(n_readout_qubits)):
for i in list(range(2**(ctl_bit))):
qc.append(ctrl_s, [ctl_bit, n_readout_qubits])
この後に逆量子フーリエ変換を実行するのですが、その前に少し確認です。QiskitでQFT(num_qubits=3, inverse=True, do_swaps=True).decompose().draw('mpl')を実行すると逆量子フーリエ変換の回路が以下の様に表示されます。
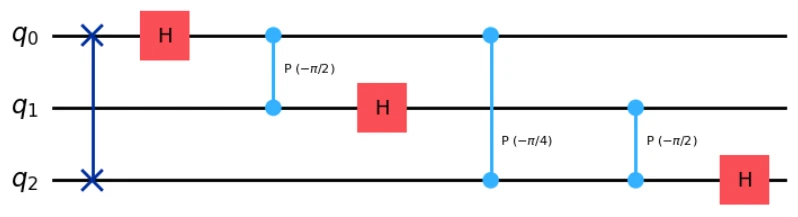
この変換の順序に合わせて読み出しレジスタの状態を用意する必要があるため、今回はSWAPゲートを適用せずにそのまま回路に接続します。
iqft = QFT(num_qubits=n_readout_qubits, inverse=True, do_swaps=True)
qc.append(iqft, [0, 1, 2])
qc.measure([0, 1, 2], [0, 1, 2])
量子フーリエ変換、逆量子フーリエ変換を実装する場合は適用の順序に注意する必要があります。今回のケースでは各量子ビットに適用された制御$S$ゲートの規則を考慮して逆量子フーリエ変換の回路を接続することで想定通りの結果が得られます。
ここまでの回路をqc.draw('mpl')すると以下の通りとなります。
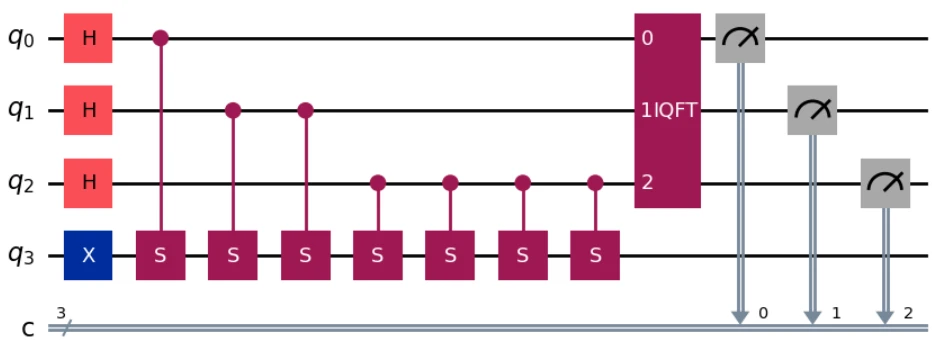
では、量子回路を実行しましょう。
pub = (qc, None)
job = sampler.run([pub], shots=1024)
result=job.result()[0]
print(result.data.c.get_counts())
# Output
# Counter({'010': 1024})
結果は010となります。今回読み出しレジスタの量子ビットの数は$n$であったため、$\phi = 2/2^3 = 1/4$がこの回路により推定されたことになります。
つまり$S$ゲートの$\ket{1}$に対する固有値は$e^{2\pi i \phi} = e^{\pi i /2}$と推定されたことになります。確かに以下の理論式と矛盾が無いです。
無事に量子位相推定を実行できました!
$$ S |1\rangle = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/2} \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = e^{i\pi/2} |1\rangle $$
Amazon Braket学習コース
この記事で登場する、量子ゲートや量子回路など、量子コンピュータの基本的な知識や、Amazon Braketの使い方についてはこちらのコースで効率的に学べます。
量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう!
はじめての量子コンピューター入門【基礎知識・Qiskitでの実装・量子機械学習 全て学べる】
量子コンピューターの入門コースを作成しました。このコースにより、量子コンピューターの基礎知識、Qiskitでの実装、量子機械学習について学べます。

