IBM 量子開発者認定資格 v2.X sample問題集の解説 その1

2025年、新しいQiskitのバージョンに対応した資格である、「IBM Certified Quantum Computation using Qiskit v2.X Developer - Associate」がリリースされました。

この資格を取得することでqiskitや量子プログラミングに関する知識を証明することが可能です。

この認定を得るためには、上記リンクに記載がある通り、“Exam C1000-179: Fundamentals of Quantum Computing Using Qiskit v2.X Developer”という試験に合格する必要があります。 IBMはこの試験に関するsample問題集も公開しており、上記URLリンク内の「Sample Test」で公開されています。 ただ、こちらのSample問題集では解説は特に記載されていないため、なるべく分かりやすく解説を記載します。このページでは1 ~ 10問までの解説を記載しています。11 ~ 21問の解説についてはこちらのページをご参照ください。

はじめての量子コンピューター入門【基礎知識・Qiskitでの実装・量子機械学習 全て学べる】

量子コンピューターの入門コースを作成しました。このコースにより、量子コンピューターの基礎知識、Qiskitでの実装、量子機械学習について学べます。

QiskitCourseJa

Amazon Braket学習コース

また、AWSでの量子コンピューティングサービスであるAmazon braketについての学習コースを作成しました。

QiskitCourseJa

量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう！

問題1:

Which one of the following code fragments will generate the given output?

[[ 1.+0.j  0.+0.j  0.+0.j  0.+0.j]
 [ 0.+0.j -1.+0.j  0.+0.j  0.+0.j] 
 [ 0.+0.j  0.+0.j  1.+0.j  0.+0.j] 
 [ 0.+0.j  0.+0.j  0.+0.j -1.+0.j]]

選択肢:

  • A.
p = Pauli('IZ') 
print(p.to_matrix())

　　

  • B.
p = Pauli('-II') 
print(p.to_matrix())

　　

  • C.
p = Pauli('-ZI') 
print(p.to_matrix())

　　

  • D.
p = Pauli('ZZ') 
print(p.to_matrix())

回答: A

解説: どのコードが問題分で表示されている行列を生成するかという問題ですね。 コードで登場しているPauli() は演算子を表現するためのクラスです。 選択肢にPauli('IZ') など登場していますが、これは$I \otimes Z$のテンソル積を表しています。 行列のテンソル積の計算は以下の様に表せます。

$$ \begin{align*} X \otimes Y = \begin{pmatrix} X_{11} Y & X_{12} Y \\ X_{21} Y & X_{22} Y \end{pmatrix} &= \begin{pmatrix} X_{11} Y_{11} & X_{11} Y_{12} & X_{12} Y_{11} & X_{12} Y_{12} \\ X_{11} Y_{21} & X_{11} Y_{22} & X_{12} Y_{21} & X_{12} Y_{22} \\ X_{21} Y_{11} & X_{21} Y_{12} & X_{22} Y_{11} & X_{22} Y_{12} \\ X_{21} Y_{21} & X_{21} Y_{22} & X_{22} Y_{21} & X_{22} Y_{22} \end{pmatrix} \end{align*} $$

ここで$X, Y$は以下の通りです。

$$ X = \begin{pmatrix} X_{11} & X_{12} \\ X_{21} & X_{22} \end{pmatrix}, \quad Y = \begin{pmatrix} Y_{11} & Y_{12} \\ Y_{21} & Y_{22} \end{pmatrix} $$ 　　

さらに各コードに登場しているゲート$I, Z$は以下となります。

$$ I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $$ これらを考慮することにより、それぞれの選択肢に対応する行列を計算してみましょう。
Aは$I \otimes Z$を表しており、計算すると以下が得られます。 $$ I \otimes Z = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} $$ これは問題で表示されている行列と一致しているので、正解となります。
残りの選択肢はそれぞれ以下の様に計算でき、問題で表示されている行列と一致していないことが確かめられます。
Bについては$-I \otimes I$を表しており、以下が得られます。 $$ -I \otimes I = \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} $$
Cについては$-Z \otimes I$を表しており、以下が得られます。 $$ -Z \otimes I = \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$
Dについては$Z \otimes Z$を表しており、以下が得られます。 $$ Z \otimes Z = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$
　　
　　
　　

問題2:

Applying the Qiskit T Gate to a qubit in state |1> introduces which global phase?

選択肢:

  • A. $\pi/2$ phase

  • B. $- \pi/2$ phase 　　

  • C. $- \pi/4$ phase

  • D. $\pi/4$ phase

回答: D

解説: Tゲートは|1>のグローバル位相をどれだけ変化させるか？という問題ですね。Z軸を軸として回転を施すゲートは、T、S、Zゲートなど存在しており、これらは|1>をそれぞれ$\pi/4、\pi/2、\pi$の位相だけ状態を回転させます。このため、正解はDとなります。 　　
　　
　　

問題3:

Given the following code fragment, what is the approximate probability that a measurement would result in a bit value of 1?

from qiskit import QuantumCircuit 
import numpy as np 
qc = QuantumCircuit(1) 
qc.reset(0) 
qc.ry(np.pi / 2, 0) 
qc.measure_all()

選択肢:

  • A. 0.8536
  • B. 1.0
  • C. 0.1464
  • D. 0.5

回答: D

解説: 問題文のコードを実行した時に、|1>を観測する確率は？という問題ですね。 問題文のコードでは、QuantumCircuit(1)を使って量子ビットを1つ定義しています。 この時点では、量子ビットは下記のような|0>の状態、つまり何度観測しても|0>が確認される状態となっています。ちなみに、この状態ではZ軸からの傾きを表すθは0となります。

0状態
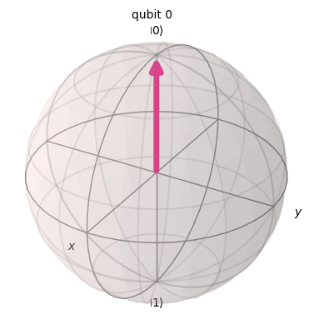
この後、qc.reset(0)が適用されていますが、これは0番目の量子ビットを|0>状態に変更する処理を表しており、既に|0>状態のため、特に変化はおきません。
そして、qc.ry(np.pi / 2, 0)の箇所でその量子ビットをY軸周りに$θ = \pi / 2$だけ回転を施しています。 これを実施した時に量子ビットは下記のような状態になります。

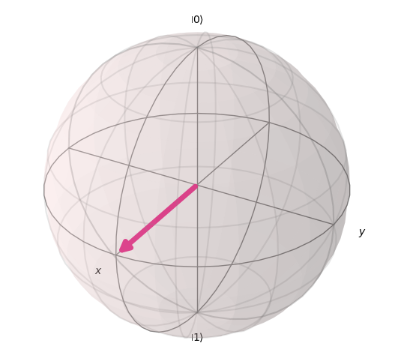
plus状態

このように、ブロッホ球では、ベクトルはθの値に応じて|0>または|1>の方向に傾きます。そして|0>の方向への傾きが大きい場合（つまり、θ < π/2）、|0>が観測される確率が増加し、|1>が観測される確率が減少します。逆に、|1>の方向への傾きが大きい場合（つまり、θ > π/2）、|1>が観測される確率が増加し、|0>が観測される確率が減少します。この場合、図に示されているように、|0>と|1>ちょうど真ん中を指しているため、|0>、|1>が観測される確率はそれぞれ1/2となります。したがって、正しい答えはDとなります。

　　
　　
　　

問題4:

Which one of the following images is the output from the code below:

from qiskit import * 
qubits = QuantumRegister(2) 
clbits = ClassicalRegister(2) 
circuit = QuantumCircuit(qubits, clbits) 
(q0, q1) = qubits 
(c0, c1) = clbits 
circuit.h(q0) 
circuit.measure(q0, c0) 
with circuit.if_test((c0, 1)) as else_: 
    circuit.h(q1) 
with else_: 
    circuit.x(q1) 
circuit.measure(q1, c1) 

circuit.draw(output="mpl")

選択肢:

  • A.
    a
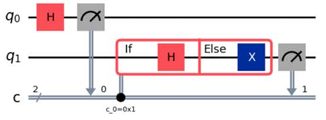
  • B.
    b
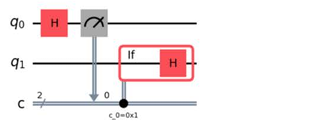
  • C.
    c
  • D.
    d

回答: A

解説: コードを実行した際に表示される量子回路はどれか？という問題ですね。
まずは問題のコードをみてみましょう。

from qiskit import * 
qubits = QuantumRegister(2) 
clbits = ClassicalRegister(2) 
circuit = QuantumCircuit(qubits, clbits) 
(q0, q1) = qubits 
(c0, c1) = clbits

上記の部分で、量子ビット $q0, q1$と古典ビット $c0, c1$を定義しています。

circuit.h(q0) 
circuit.measure(q0, c0)

次に上記の部分で、 $q0$にアダマールゲートを適用、観測し結果を $c0$に格納しています。

with circuit.if_test((c0, 1)) as else_: 
    circuit.h(q1) 
with else_: 
    circuit.x(q1) 
circuit.measure(q1, c1)

そして観測された $c0$で分岐処理をしています。これは $c0$ が1であった場合は、Hゲートを $q1$に適用し、そうでない場合はXゲートを $q1$に適用することを意味しています。

circuit.draw(output="mpl")

最終的にはこちらで回路を表示しています。
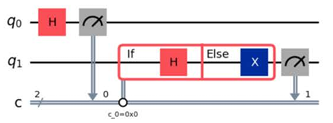
これを踏まえて選択肢を見ていきましょう。 まずElseの記載が無いBは誤りということが分かります。
また、ifでXゲートを適用してしまっているCも誤りとわかります。
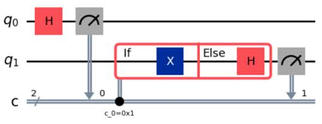
残っているのはAとDで、これらは図の中での一番下の式が異なります。 Aにはc_0=0x1、Dにはc_0=0x0と記載があります。0x1は16進数の1、0x0は16進数の0を表しており、今回はコードで

with circuit.if_test((c0, 1)) as else_:

と記載があるためAが正解となります。

　　
　　
　　

問題5:

Given the code fragment below, which image is the expected output?:

from qiskit.quantum_info import Statevector 
from qiskit.visualization import plot_histogram 
state = Statevector([0.+0.j, 0.+0.j, 0.70710678+0.j, 0.+0.j, 0.+0.j, -0.70710678+0.j, 0.+0.j, 0.+0.j]) 
counts = state.sample_counts(shots=1024) 
plot_histogram(counts)

選択肢:

  • A.
    a
  • B.
    b
  • C.
    c
  • D.
    d

回答: C

解説: コード実行時の結果で正しいものを選びなさいという問題ですね。

state = Statevector([0.+0.j, 0.+0.j, 0.70710678+0.j, 0.+0.j, 0.+0.j, -0.70710678+0.j, 0.+0.j, 0.+0.j])

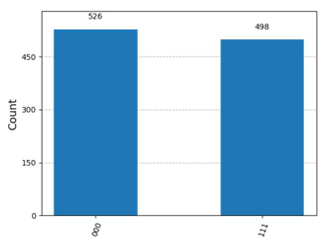
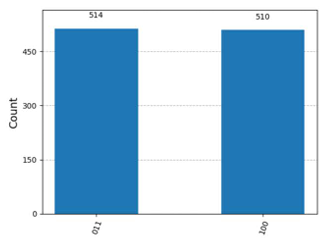
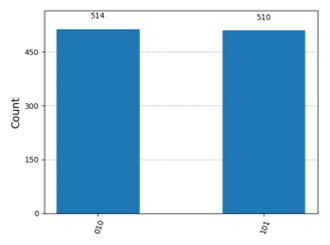
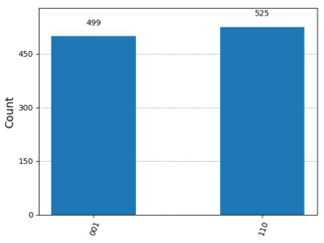
コード内に上記の記載がありますが、ベクトルの要素が$8=2^3$個あるため3量子ビットの状態をこのStatevector()で表していることがわかります。各要素については先頭から順に|000>,|001>,|010>,|011>,|100>,|101>,|110>,|111>の係数に対応しています。これを考慮すると、|010>と|101>の係数がそれぞれ0.70710678+0.j、-0.70710678+0.jとなっていることがわかります。これら係数の絶対値の2乗は観測確率となりますがそれぞれ絶対値が同じ大きさのため、|010>と|101>が同じ割合で観測されることになります。
これに対応した図はCのみのため、Cが正解となります。

　　
　　
　　

問題6:

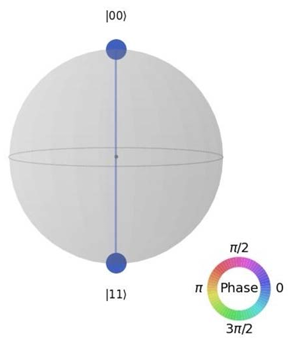
Which one of the following code fragments will generate the given qsphere representation visualization?
Note: the circles on the qsphere are the same color.

a

選択肢:

  • A.
qc = QuantumCircuit(2) 
qc.h(0) 
qc.z(0) 
qc.cx(0, 1) 
state = Statevector(qc) 
plot_state_qsphere(state)

　　

  • B.
qc = QuantumCircuit(2) 
qc.h(0) 
qc.z(0) 
qc.x(1) 
qc.cx(0, 1) 
state = Statevector(qc) 
plot_state_qsphere(state)

　　

  • C.
qc = QuantumCircuit(2) 
qc.x(1) 
qc.h(0) 
qc.cx(0, 1) 
state = Statevector(qc) 
plot_state_qsphere(state)

　　

  • D.
qc = QuantumCircuit(2) 
qc.h(0) 
qc.cx(0, 1) 
state = Statevector(qc) 
plot_state_qsphere(state)

回答: D

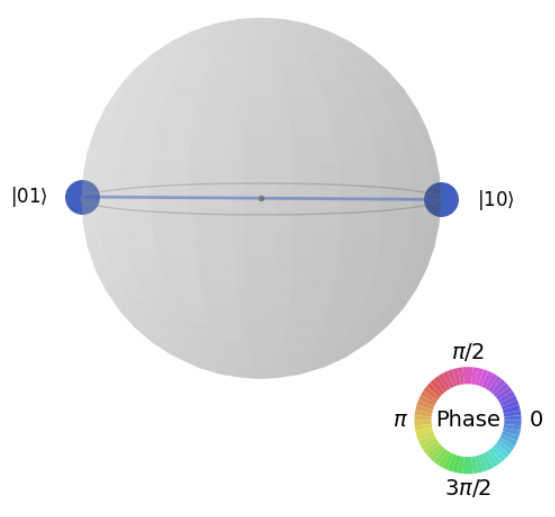
解説: どのコードが表示されている画像を生成しますか？という問題ですね。画像は|00>と|11>という状態が表示されており、同じ青色で繋がっております。plot_state_qsphere()で同じ色で繋がっていることは、同じ位相であることを意味します。これはつまり片方の状態に $e^{i \pi / 3}$のような係数やマイナスが付かないことを意味し、数式では以下の様に記載できます。

$$ \begin{align*} |\Phi^+\rangle &= \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle) \\ \end{align*} $$

この状態は以下の様に、初期状態の$|0\rangle \otimes |0\rangle$について、片方のビットにHゲートを適用し、Hゲートをかけたビットを制御ビットとしてCXゲートを適用することで得られます。 $$ |0\rangle \otimes |0\rangle \xrightarrow{H_0} \frac{|0\rangle + |1\rangle}{\sqrt{2}} \otimes |0\rangle \xrightarrow{\text{CX}_{0,1}} \frac{|0\rangle \otimes |0\rangle + |1\rangle \otimes |1\rangle}{\sqrt{2}} $$ この適用規則が記載されているのはDのみのため、Dが正解となります。
他の選択肢については、実行すると以下の様に別の状態が表示されます。

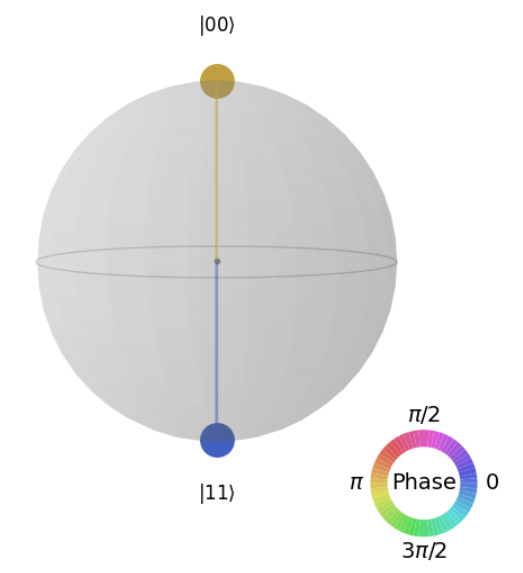
Aについては、正解のDと比べてqc.z(0)が追加されています。qc.z(0)は状態$|1\rangle$の位相を反転させます。これにより$\frac{1}{\sqrt{2}} (|00\rangle - |11\rangle)$と、位相が反転して、たし合わされた状態が実現します。表示される図は以下の通りです。

a

Bについては、Aのコードに追加でqc.x(1)が適用されており、CXゲートが適用される直前、1番目の量子ビットが0から1に変換されています。このため表示される図は以下の通りです。
b

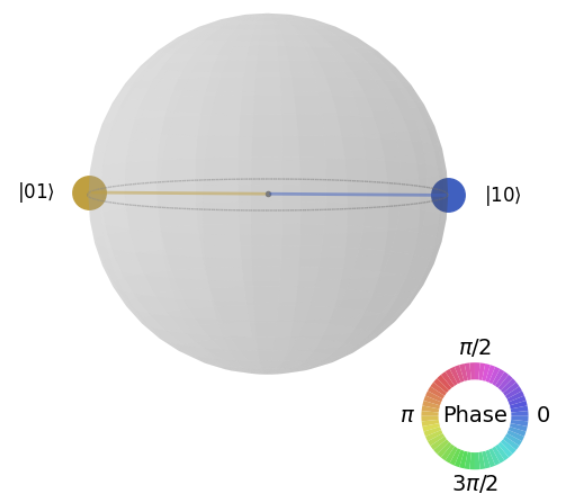
Cについては、正解のDと比べてqc.x(1)が事前に適用されており、1番目の量子ビットが0から1に変換されています。このため表示される図は以下の通りです。
b

　　
　　
　　

問題7:

Given the code fragment below, which of the following code fragments creates a rotation gate with an angle with an initially undefined value?

from qiskit.circuit import QuantumCircuit, Parameter, ParameterExpression 
qc = QuantumCircuit(1)

選択肢:

  • A.
theta = 3.14 
qc.rx(3.14, 0)

　　

  • B.
theta = Parameter('theta') 
qc.rx(theta, 0)

　　

  • C.
qc.rx('theta', 0)

　　

  • D.
qc.rx(ParameterExpression('theta'), 0)

回答: B

解説: 次のうちどのコードが、角度が変数の回転ゲートを作成しますか？という問題ですね。QiskitではParameter()を用いることで、変数を持つ量子回路を定義可能です。この機能を持ちいることで、回路を定義した後、変数に様々な値を代入して量子回路を実行することが可能となります。この関数の正しい利用方法はBとなり、これが正解となります。
Aについては角度を変数として回転ゲートを定義できていないため不正解です。
C、Dは実行するとエラーとなります。

　　
　　
　　

問題8:

Which one of the following types of register stores the result of a measured circuit?

選択肢:

  • A. Ancilla register 　　

  • B. Quantum register 　　

  • C. Classical register 　　

  • D. Circuit register 　　

回答: C

解説: 次のうちどれが回路の測定結果を保存しますか？という問題ですね。Quantum register、Classical register、Ancilla registerについての説明はこちらに記載があります。
CのClassical registerは計算後の測定結果を保存するレジスタで今回はこちらが正解となります。
AのAncilla registerは主にエラー訂正やアルゴリズム実装の補助に使われるレジスタです。
BのQuantum registerは量子ビットを保持するレジスタです。
DのCircuit registerはqiskit.circuitには存在しません。

　　
　　
　　

問題9:

Given the code fragment below, which one of the following images could be produced?

from qiskit import QuantumCircuit 
from qiskit import generate_preset_pass_manager 
qc = QuantumCircuit(2) 
qc.h(0) 
qc.cx(0,1) 
pass_manager = generate_preset_pass_manager( 
    optimization_level=3, 
    coupling_map=[[0, 1], [1, 2]] , 
    basis_gates=['h', 'swap', 'cx'], 
    initial_layout=[0, 2] ) 
tqc = pass_manager.run(qc) 
tqc.draw(output="mpl")

選択肢:

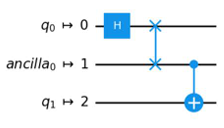
  • A.
    a
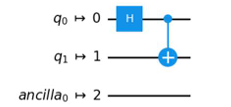
  • B.
    b
  • C.
    c
  • D.
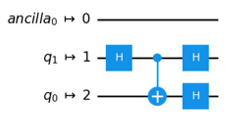
    d

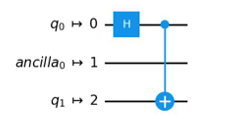
回答: A

解説: コード実行時の出力で正しいものを選びなさいという問題ですね。
まずはコードを確認してみましょう。

from qiskit import QuantumCircuit 
from qiskit import generate_preset_pass_manager 
qc = QuantumCircuit(2) 
qc.h(0) 
qc.cx(0,1)

この部分でHゲートと、CXゲートを適用する量子回路を定義しています。ちなみにこれはベル状態を生成する回路ですね。

pass_manager = generate_preset_pass_manager( 
    optimization_level=3, 
    coupling_map=[[0, 1], [1, 2]] , 
    basis_gates=['h', 'swap', 'cx'], 
    initial_layout=[0, 2] )

generate_preset_pass_manager()は、実際の量子コンピューターや、様々な制約がある環境用に量子回路を変換してくれる関数です。また、このコードの様に実際の量子コンピューターを指定せずとも、様々な制約を自ら設定し、仮想的な環境を定義することが可能です。
これの引数について見ていきましょう。 coupling_map=[[0, 1], [1, 2]]は、0番と1番、もしくは1番と2番の（仮想的な）物理量子ビットでのみ接続があることを示しています。これを例えば図で表すと以下の通りです。

d

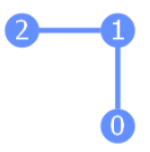
この通り、0番と2番の量子ビット間では接続がありません。このため、0番と2番を対象としてCXゲートを適用することはできません。これがこの問題で重要なポイントとなります。basis_gates=['h', 'swap', 'cx']はこの仮想的な環境でHゲート、Swapゲート、CXゲートのみがサポートされるという制約を設定しています。 またinitial_layout=[0, 2]により、qcで定義されている量子ビットq0を、0番の物理量子ビット上にマッピングし、量子ビットq1を2番の物理量子ビット上にマッピングしてから計算を行う設定を与えています。 なぜわざわざこれらのような制約を与えているのかと疑問に思われる方もいるかもしれません。量子コンピューター実機を扱う際はこれらのような制約が存在している場合がよくあります。したがって、ローカル環境であらかじめ制約を設定して計算を行うことは、実機での動作を見据えた有効な検証手段となります。 optimization_level=3は、この環境用にpass_managerが量子回路を変換する際にどれほどの最適化レベルを設定するかを意味しています。3は最高レベルを示します。

tqc = pass_manager.run(qc) 
tqc.draw(output="mpl")

そしてこの部分で元々定義していた回路qcをpass_managerで仮想的な環境に合わせた量子回路tqcに変換し、回路を出力しています。 では、選択肢を見ていきましょう。
Bはinitial_layout=[0, 2]の設定である、量子ビットq0を0番の物理量子ビット上に、量子ビットq1を2番の物理量子ビット上にマッピングするという設定が反映されていないため誤りです。
Cは回路の一番最後に、定義していないHゲートが挿入されてしまっているため誤りです。
Dはinitial_layout=[0, 2]の設定である、量子ビットq0を0番の物理量子ビット上に、量子ビットq1を2番の物理量子ビット上にマッピングするという設定も反映されており、正解に見えるのですが、既に説明した通り今回0番と2番の物理量子ビットにCXゲートを適用することができません。generate_preset_pass_manager()はこのような場合、選択肢AのようにSwapゲートを適用し量子ビットを入れ替えることで、回路を実行可能な形にしてくれます。このためDは誤りで、Aは正解となります。generate_preset_pass_manager()の利用方法についてはこちらのコースも参考にしてみてください。

　　
　　
　　

問題10:

Which three of the following are job execution modes in Qiskit Runtime?

選択肢:

  • A. classical

  • B. session

  • C. parallel

  • D. quantum

  • E. batch

  • F. single job

　　

回答: B, E, F

解説: Qiskit Runtimeの実行モードに該当するのはどれか？という問題ですね。Qiskit Runtimeの実行モードについてはこちらに記載があります。これに記載されているように、Qiskit Runtimeの実行モードに該当するのはsession, batch, single jobの3つとなりB、E、Fが正解となります。では、各モードについて以下で説明します。
single jobモードは最も単純なモードです。単発のジョブを実行してみる場合などに便利です。
batchモードは複数のジョブをまとめて実行するのに有効なモードです。ただしバッチ処理として扱われるため、ジョブが送信された順序通りに実行される保証は無いことに注意が必要です。
sessionモードでは、システムを独占的に使用できる専用の時間枠が設けられます。VQCや、VQEなどの変分アルゴリズムでは、古典コンピューターでの計算と量子コンピューターでの計算が交互に行われますが、計算のたびに他のユーザーのジョブを待機していると非常に時間がかかってしまいます。このモードを用いることで、このような問題は発生せずに、変分アルゴリズムを高速で実行できるようになります。

11 ~ 21問の解説についてはこちらのページをご参照ください。

はじめての量子コンピューター入門【基礎知識・Qiskitでの実装・量子機械学習 全て学べる】

量子コンピューターの入門コースを作成しました。このコースにより、量子コンピューターの基礎知識、Qiskitでの実装、量子機械学習について学べます。

QiskitCourseJa

Amazon Braket学習コース

また、AWSでの量子コンピューティングサービスであるAmazon braketについての学習コースを作成しました。

QiskitCourseJa

量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう！