IBM 量子開発者認定資格 sample問題集の解説 その1
別ページで量子コンピュータでは、古典コンピュータとは異なるプログラムである、量子プログラムを実装する必要があると記載しました。ここで、この量子プログラムに関する資格「IBM Certified Associate Developer - Quantum Computation using Qiskit v0.2X」をIBMが2021年から提供しています（早い）。 https://www.ibm.com/training/certification/ibm-certified-associate-developer-quantum-computation-using-qiskit-v02x-C0010300
この資格を取得することでqiskitや量子プログラミングに関する知識を証明することが可能です。
この認定を得るためには、上記URLに記載がある通り、“Exam C1000-112: Fundamentals of Quantum Computation Using Qiskit v0.2X Developer”という試験に合格する必要があります。
IBMはこの試験に関するsample問題集も公開しており、上記URLサイト内の「Sample Test」で公開されています。
ただ、こちらのSample問題集では解説は特に記載されていないため、なるべく分かりやすく解説を記載します。このページでは1 ~ 10問までの解説を記載しています。11 ~ 20問の解説についてはこちらのページをご参照ください。
試験対策としては下記のような問題集も是非是非、ご活用ください。
英語版問題集
日本語版問題集
Amazon Braket学習コース
また、AWSでの量子コンピューティングサービスであるAmazon braketについての学習コースを作成しました。
量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう！
問題1:
Which statement will create a quantum circuit with four quantum bits and four classical bits?
選択肢:
- A. QuantumCircuit(4, 4)
- B. QuantumCircuit(4)
- C. QuantumCircuit(QuantumRegister(4, ‘qr0’), QuantumRegister(4, ‘cr1’))
- D. QuantumCircuit([4, 4])
回答: A
解説: 4つの量子ビット、4つの古典ビットを持つ量子回路を作成しなさいという問題ですね。 別ページですでに、量子ビットについては少し解説していますが、量子回路ではよく観測用のビットとして古典ビットも定義することがあります。Qiskitでは下記の様にして量子ビット、古典ビットを定義可能です。この例では変数qcにx個の量子ビット、y個の古典ビットを持つ回路を定義しています。
qc = QuantumCircuit(x, y)
このため、正解はAとなります。他の選択肢について、Bでは量子ビット4つのみが定義され、古典ビットは定義されません。CではQuantumRegisterが利用されているため古典ビットが定義されていません。Dは実行するとエラーとなります。
問題2:
Given this code fragment, what is the probability that a measurement would result in |0> ?
qc = QuantumCircuit(1)
qc.ry(3 * math.pi/4, 0)
選択肢:
- A. 0.8536
- B. 0.5
- C. 0.1464
- D. 1.0
回答: C
解説:
問題文のコードを実行した時に、|0>を観測する確率は？という問題ですね。
問題文のコードでは、問題1で登場したQuantumCircuit()を使って量子ビットを1つ定義しています。
この時点では、量子ビットは下記のような|0>の状態、つまり何度観測しても|0>が確認される状態となっています。ちなみに、この状態ではZ軸からの傾きを表すθは0となります。
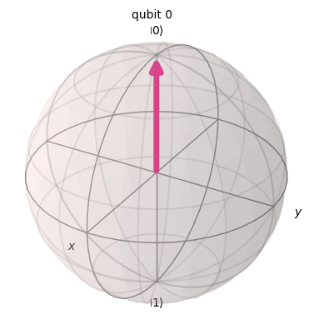
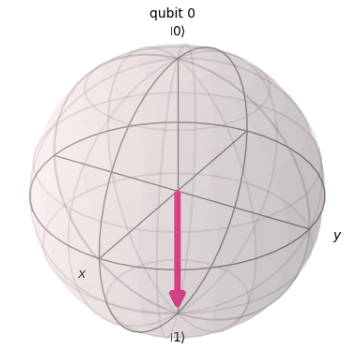
そして、qc.ry(3 * math.pi/4, 0)の箇所でその量子ビットをY軸周りに$θ = 3 \pi / 4$だけ回転を施しています。
これを実施した時に量子ビットは下記のような状態になります。
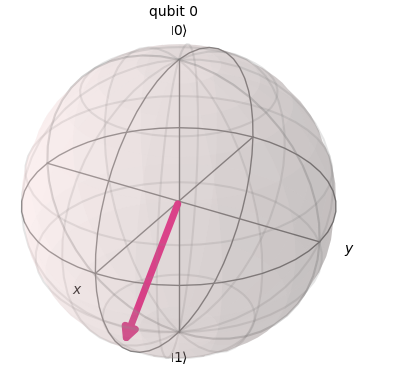
このように、ブロッホ球では、ベクトルはθの値に応じて|0>または|1>の方向に傾きます。そして|0>の方向への傾きが大きい場合（つまり、θ < π/2）、|0>が観測される確率が増加し、|1>が観測される確率が減少します。逆に、|1>の方向への傾きが大きい場合（つまり、θ > π/2）、|1>が観測される確率が増加し、|0>が観測される確率が減少します。この場合、図に示されているように、|1>の方向への傾きが大きいため、|0>が観測される確率が減少します。ただし、|1>の状態と完全に一致しているわけではないため、|0>が観測される確率は0にはなりません。したがって、正しい答えはCとなります。
もちろん、qc.ry(3*math.pi/4, 0)を行列として表現し、手作業でRY|0>の値を計算し、その確率を求めることもできます。行列とベクトルで表現されたRY|0>は以下の通りで、先ほどの結論と同じとなります。
$$ R_{y(3\pi/4)} |0\rangle = \begin{bmatrix} \cos\frac{3\pi}{8} & -\sin\frac{3\pi}{8} \\ \sin\frac{3\pi}{8} & \cos\frac{3\pi}{8} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \cos\frac{3\pi}{8} |0\rangle + \sin\frac{3\pi}{8} |1\rangle $$
$$
\left|\cos\frac{3\pi}{8}\right|^2 \approx 0.1464
$$
ただし、
$$
R_{y(\theta)} =
\begin{bmatrix}
\cos\frac{\theta}{2} & -\sin\frac{\theta}{2} \\
\sin\frac{\theta}{2} & \cos\frac{\theta}{2}
\end{bmatrix}
$$
問題3:
Assuming the fragment below, which three code fragments would produce the circuit illustrated?
inp_reg = QuantumRegister(2, name='inp')
ancilla = QuantumRegister(1, name='anc')
qc = QuantumCircuit(inp_reg, ancilla)
# Insert code here
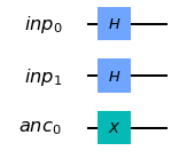
選択肢:
- A.
qc.h(inp_reg)
qc.x(ancilla)
qc.draw()
- B.
qc.h(inp_reg[0:2])
qc.x(ancilla[0])
qc.draw()
- C.
qc.h(inp_reg[0:1])
qc.x(ancilla[0])
qc.draw()
- D.
qc.h(inp_reg[0])
qc.h(inp_reg[1])
qc.x(ancilla[0])
qc.draw()
- E.
qc.h(inp_reg[1])
qc.h(inp_reg[2])
qc.x(ancilla[1])
qc.draw()
- F.
qc.h(inp_reg)
qc.h(inp_reg)
qc.x(ancilla)
qc.draw()
回答: A,B,D
解説: 選択肢のうち、どのコードを追加すれば図に記載されている回路を生成できるか？という問題ですね。
まずは問題文のコードを見ていきましょう。このコードではinp_regという変数にinpという名前で量子ビットを2ビット、ancillaにancという名前で量子ビットを1ビット定義し量子回路を作成しています。
図を見てみると、inp_regの0,1番目のビットにHゲートが、ancillaの0番目のビットにxゲートが適用されており、これを実現するコードが正解となります。一つずつ見ていきましょう。
Aはinp_reg全体にHゲートを、ancilla全体にXゲートを適用しているため、正解となります。
Bはinp_regの0,1番目のビットにHゲートを、ancillaの0番目のビットにXゲートを適用しているため、正解となります。
Cはinp_regの0番目のビットにHゲートを、ancillaの0番目のビットにXゲートを適用しており、inp_regの1番目のビットにHゲートを適用できていないため不正解となります。
Dはinp_regの0,1番目のビットにHゲートを、ancillaの0番目のビットにXゲートを適用しているため、正解となります。
Eはinp_regの1,2番目のビットにHゲートを、ancillaの1番目のビットにXゲートを適用しており、不正解となります。
Fはinp_reg全体にHゲートを2回、ancilla全体にXゲートを適用しているため、不正解となります。 Hゲートを2回適用する必要はありません。
問題4:
Given an empty QuantumCircuit object, qc, with three qubits and three classical bits, which one of these code fragments would create this circuit?
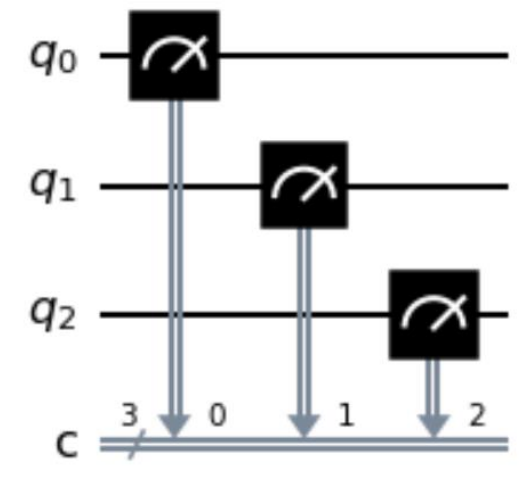
選択肢:
- A. qc.measure([0,1,2], [0,1,2])
- B. qc.measure([0,0], [1,1], [2,2])
- C. qc.measure_all()
- D. qc.measure(0,1,2)
回答: A
解説:
3つの量子ビット、3つの古典ビットを持つ量子回路において、問題文の回路を作成するコードはどれか？という問題ですね。問題文のコードでは3つの量子ビットが、3つの古典ビットを用いて観測されています。1つずつ見ていきましょう。
Aは0,1,2番目の量子ビットを、0,1,2番目の古典ビットで観測を行うというコードになっており、正解となります。
Bはフォーマットが間違っており、実行するとエラーとなります。
Cはqc.measure_all()を用いており、こちらを用いると、予め用意していた古典ビットは使われないため、下記のような回路になります。よってかなり近いのですが、こちらは不正解となります。
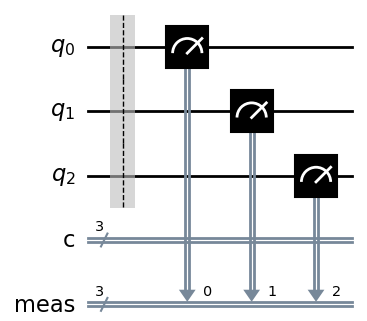
問題5:
Which code fragment will produce a maximally entangled, or Bell, state?
選択肢:
- A.
bell = QuantumCircuit(2)
bell.h(0)
bell.x(1)
bell.cx(0, 1)
- B.
bell = QuantumCircuit(2)
bell.cx(0, 1)
bell.h(0)
bell.x(1)
- C.
bell = QuantumCircuit(2)
bell.h(0)
bell.x(1)
bell.cz(0, 1)
- D.
bell = QuantumCircuit(2)
bell.h(0)
bell.h(0)
回答: A
解説: どのコードが、ベル状態を作るか？という問題ですね。ベル状態は、一方のビットを観測することで他方のビットの状態が決定される下記のような状態を指します。
$$
\begin{align*}
|\Phi^+\rangle &= \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle), \\
|\Phi^-\rangle &= \frac{1}{\sqrt{2}} (|00\rangle - |11\rangle), \\
|\Psi^+\rangle &= \frac{1}{\sqrt{2}} (|01\rangle + |10\rangle), \\
|\Psi^-\rangle &= \frac{1}{\sqrt{2}} (|01\rangle - |10\rangle).
\end{align*}
$$
例えば上記に記載されている$|\Psi^+\rangle$、$|\Psi^-\rangle$では、0ビット目が1と観測された場合、その瞬間1ビット目が0となることが確定します。
この問題において、ベル状態を作成するにはCXゲートを使用する必要があります。CXゲートとは制御ビット、ターゲットビットの2量子ビットを扱ったゲートであり、制御ビットのビットが1の場合、ターゲットビットにXゲートを適用し、0の場合は何もしないゲートとなります。
このため、CXゲートが現われていない、C、Dがこの時点で不正解と分かります。
そしてベル状態を作成するには、制御ビットは$|+\rangle = \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle)$ や $|-\rangle = \frac{1}{\sqrt{2}} (|0\rangle - |1\rangle)$ のように、0または1のいずれかで観測される確率が1/2である状態である必要があり、ターゲットビットは$|0\rangle$または$|1\rangle$の明確な状態である必要があります。
Aでは、0番目の量子ビットがHゲートにより$|+\rangle$状態に変換され、1番目の量子ビットが明確な状態$|1\rangle$にあり、これにCXゲートが適用されているため、正解となります。
Bでは、0、1番目の量子ビットが両方|0>の状態で、CXゲートが適用されており、こちらは不正解となります。
問題6:
Given this code, which two inserted code fragments result in the state vector represented by this Bloch sphere?
qc = QuantumCircuit(1,1)
# Insert code fragment here
simulator = Aer.get_backend('statevector_simulator')
job = execute(qc, simulator)
result = job.result()
outputstate = result.get_statevector(qc)
plot_bloch_multivector(outputstate)
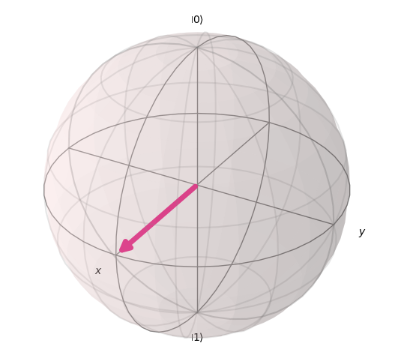
選択肢:
- A. qc.h(0)
- B. qc.rx(math.pi / 2, 0)
- C. qc.ry(math.pi / 2, 0)
- D. qc.rx(math.pi / 2, 0)
qc.rz(-math.pi / 2, 0) - E. qc.ry(math.pi, 0)
回答: A, C
解説:
選択肢のうち、どのコードを追記すれば図で表示されているブロッホ球の状態になるか？という問題ですね。コードを見てみるとQuantumCircuit(1,1) で量子ビットを定義しており、その後にコードを追記する箇所があります。QuantumCircuit() で定義された直後の量子ビットは|0>の状態であり、これを図のように$|+\rangle= \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle)$の状態に更新するコードが正解となるわけです。一つずつ見てみましょう。
AではHゲートを適用しており、これにより|0>は図のような$|+\rangle$の状態に量子ビットが変更されます。このためAは正解となります。
BではX軸を軸とした、π/2の回転が施され、|0>の状態の量子ビットは下記の状態に変更されます。このため不正解です。
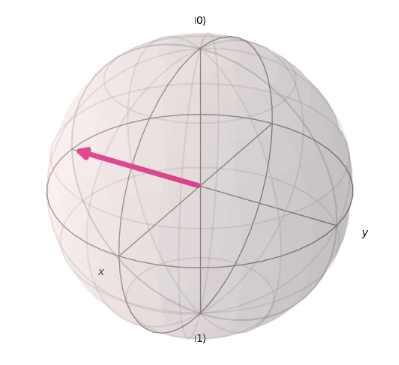
Dではqc.rx(math.pi / 2, 0)によりまず、X軸を軸とした、π/2の回転が施され、量子ビットは下記の状態に変更されます。
qc.rz(-math.pi / 2, 0)によりZ軸を軸とした、-π/2の回転が施され、最終的に下記の状態となります。このためDは不正解となります。
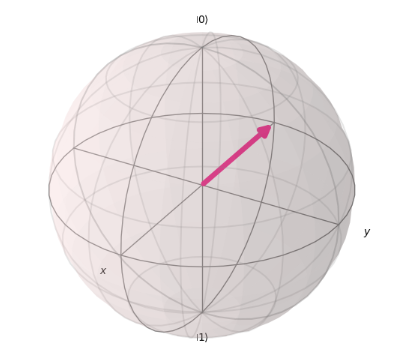
問題7:
S-gate is a Qiskit phase gate with what value of the phase parameter?
選択肢:
-
A. $\pi/4$
-
B. $\pi/2$
-
C. $\pi/8$
-
D. $\pi$
回答: B
解説:
Sゲートの位相パラメータはいくつか？という問題ですね。Z軸を軸として回転を施すゲートは、T、S、Zゲートなど存在しており、それぞれ$\pi/4、\pi/2、\pi$の位相だけ状態を回転させます。このため、正解はBとなります。
問題8:
Which two code fragments, when inserted into the code below, will produce the statevector shown in the output?
from qiskit import QuantumCircuit, Aer, execute
from math import sqrt
qc = QuantumCircuit(2)
# Insert fragment here
simulator = Aer.get_backend('statevector_simulator')
result = execute(qc, simulator).result()
statevector = result.get_statevector()
print(statevector)
Output:
[0.707+0.j 0.+0.j 0.+0.j 0.707+0.j]
選択肢:
- A.
v = [1/sqrt(2), 0, 0, 1/sqrt(2)]
qc.initialize(v,[0,1])
- B.
qc.h(0)
qc.cx(0,1)
- C.
v1, v2 = [1,0], [0,1]
qc.initialize(v1,0)
qc.initialize(v2,1)
- D.
qc.cx(0,1)
qc.measure_all()
- E.
qc.h(0)
qc.h(1)
qc.measure_all()
回答: A, B
解説:
Outputで表示されている状態を生成するには、どのコードを挿入すれば良いか？という問題ですね。2量子ビットなので、Outputでの状態ベクトルも4つの値を持ちますが、左から$|00\rangle$、$|01\rangle$、$|10\rangle$、$|11\rangle$の係数となります。さらに、Outputで表示されている状態は$|00\rangle$と$|11\rangle$にのみ0.707+0.jという係数を持つため、$|\Phi^+\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$という状態に該当します。ではどのコードにより、$|00\rangle$で初期化された状態をこちらの状態に変更できるでしょうか？一つずつ見ていきましょう。
Aはqc.initialize(v,[0,1])を利用して0、1番目の量子ビットを初期化しており、利用されているvについても、v = [1/sqrt(2), 0, 0, 1/sqrt(2)]とOutputの状態ベクトルと同等の値を利用しているため正解となります。
Bはqc.h(0)により、0番目の量子ビットが$|+\rangle = \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle)$に変換され、0番目を制御ビット、1番目をターゲットビットとするCXゲートが適用されています。0番目の量子ビットが$|0\rangle$として観測された場合は、CXゲートは1番目の量子ビットに何もしないため、この場合は$|00\rangle$が観測されます。0番目の量子ビットが$|1\rangle$として観測された場合は、CXゲートは1番目の量子ビットにXゲートを適用するため、この場合は$|11\rangle$が確認されます。このため、量子状態は$\frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$となり、こちらも正解となります。
Cは0番目の量子ビットをqc.initialize(v1,0)で初期化し結果的にこのビットは$|0\rangle$に、1番目の量子ビットをqc.initialize(v2,1)で初期化し結果的にこのビットは$|1\rangle$となります。出来上がった状態は$|10\rangle$となり、不正解となります。
Dは初期の$|00\rangle$の状態にCXゲートを適用していますが、0番目の量子ビット0と観測されるため、CXゲートは何もせず、$|00\rangle$の状態のままとなります。このため不正解です。
Eは0、1番目の量子ビット両方にHゲートをかけることで両方のビットが$|+\rangle$となり、両方のビットを掛け合わせることで、2量子ビットとしては$\frac{1}{2} (|00\rangle + |01\rangle + |10\rangle +|11\rangle)$という状態となります。こちらも$|\Phi^+\rangle$の状態とは別のため不正解となります。
問題9:
Which code fragment will produce a multi-qubit gate other than a CNOT ?
選択肢:
-
A. qc.cx(0,1)
-
B. qc.cnot(0,1)
-
C. qc.mct([0],1)
-
D. qc.cz(0,1)
回答: D
解説:
選択肢のうちどのコードが、CXゲートでない、多量子ビットゲートを生成しますか？という問題ですね。一つずつ見ていきましょう。
AはCXゲートを定義してしまっているため不正解となります。
Bはqc.cnot(0,1)を利用していますが、こちらもCXゲートと同等のため不正解となります。
Cはqc.mct([0],1)を利用しており、これにより多制御Toffoliゲートが定義されます。このゲートは制御ビットに複数のビットを指定することができ、制御ビットが全て$∣1\rangle$の時に、ターゲットビットにXゲートを適用します。ただし、今回は制御ビットに0番目の量子ビット単体を指定しているため、結果的にCXゲートと同様のゲートとなります。このため不正解です。
DはCZゲートを適用しており、このゲートは 制御ビットのビットが1の場合、ターゲットビットにZゲートを適用し、0の場合は何もしないゲートとなります。こちらはCXゲートとは異なる多量子ビットゲートのため、正解となります。
問題10:
Which code fragment will produce a multi-qubit gate other than a Toffoli?
選択肢:
- A.
qc.ccx(0,1,2)
- B.
qc.mct([0,1], 2)
- C.
from qiskit.circuit.library import CXGate
ccx = CXGate().control()
qc.append(ccx, [0,1,2])
- D.
qc.cry(0,1,2)
回答: D
解説:
選択肢のうちどのコードが、多制御Toffoliゲートでない、多量子ビットゲートを生成しますか？という問題ですね。多制御Toffoliゲートについては、問題9で出てきた通り、制御ビットに複数のビットを指定することができ、制御ビットが全て∣1⟩の時に、ターゲットビットにXゲートを適用するゲートとなります。一つずつ見ていきましょう。
AはCCXゲートと呼ばれ、こちらも制御ビットが全て∣1⟩の時に、ターゲットビットにXゲートを適用するゲートとなりToffoliゲートと同様のゲートのため不正解となります。ちなみにqc.ccx(0,1,2)という書き方では0、1番目の量子ビットが制御ビット、2番目の量子ビットがターゲットビットとして扱われます。
Bは多制御Toffoliゲートであり、不正解となります。ちなみにqc.mct([0,1], 2)という書き方では0、1番目の量子ビットが制御ビット、2番目の量子ビットがターゲットビットとして扱われます。
Cはfrom qiskit.circuit.library import CXGateでCXゲートをインポートしており、ccx = CXGate().control()のように.control()メソッドを利用することでCXゲートに追加の制御ビットを加えてCCXゲートとしております。このため不正解です。
Dは制御回転Yゲートと呼ばれ、制御ビットが|1>の場合、Y軸を軸とした回転を施します。こちらは多制御Toffoliゲートでない、多量子ビットゲートのため、正解となります。ちなみにqc.cry(0,1,2)という書き方では1番目の量子ビットが制御ビット、2番目の量子ビットがターゲットビットとして扱われ、回転の角度は0となります。
IBMの量子技術者認定試験問題集について
本ブログで紹介した量子開発者認定資格を目指される方のため、Udemyというサイト上にて日本語版、英語版で問題集を作りました！解説もなるべくわかりやすく作成いたしましたので、是非是非ご活用ください。
英語版問題集
日本語版問題集
Amazon Braket学習コース
AWSでの量子コンピューティングサービスであるAmazon braketについての学習コースを作成しました。
量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう！