AWSのAmazon Braketで量子機械学習：QCBM

別の記事に記載の通り、AWSの量子コンピューティングサービスであるAmazon Braketにおいては、Amazon Braket SDKと呼ばれる量子コンピューティングSDKを用いて各サービスを簡単に利用可能となります。この記事では、量子コンピュータを用いた機械学習である、量子機械学習アルゴリズムを実行する方法について説明します。

Amazon Braket学習コース

この記事で登場する、量子ゲートや量子回路など、量子コンピュータの基本的な知識や、Amazon Braketの使い方についてはこちらのコースで効率的に学べます。

https://www.udemy.com/course/quantum-computing-on-aws-for-beginners-amazon-braket/?referralCode=F361C3FD774489A1B5B8

量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。こちらも利用し、量子技術のスキルを身につけましょう！

AWSのAmazon Braketで量子機械学習: QCBM

量子機械学習アルゴリズムはいくつかの方法が提案されておりますが、今回はQuantum Circuit Born Machine (QCBM)を実行します。このアルゴリズムは、教師なし学習による生成モデルを構築できAmazon Braketのアルゴリズムライブラリに既に用意されています。
https://github.com/amazon-braket/amazon-braket-algorithm-library/tree/main/src/braket/experimental/algorithms/quantum_circuit_born_machine
今回はこちらのライブラリを使用します。

環境準備

まずは環境準備です。Amazon Braket Notebook上で実行する場合は特に実施する必要はありませんが、ご自身のPCや、サーバ上で実施する場合は、Amazon Braket SDKと、Jupyter Notebookをインストールします。またAmazon Braketアルゴリズムライブラリを利用するため、今回追加で以下も実行しています。以降の手順はJypyter Notebook上で実行しています。

git clone https://github.com/amazon-braket/amazon-braket-algorithm-library.git
cd amazon-braket-algorithm-library
pip install .

今回学習対象とするデータについて

4量子ビットが存在した場合、$2^4$通りのビット配列が表現可能です。このビット配列の中央付近にピークを持つガウス分布は以下で生成可能です。

import numpy as np
n_qubits = 4
def gaussian(n_qubits, mu, sigma):
    x = np.arange(2**n_qubits)
    gaussian = 1.0 / np.sqrt(2 * np.pi * sigma**2) * np.exp(-((x - mu) ** 2) / (2 * sigma**2))
    return gaussian / sum(gaussian)

data = gaussian(n_qubits, mu=7, sigma=2)
data = data / sum(data)

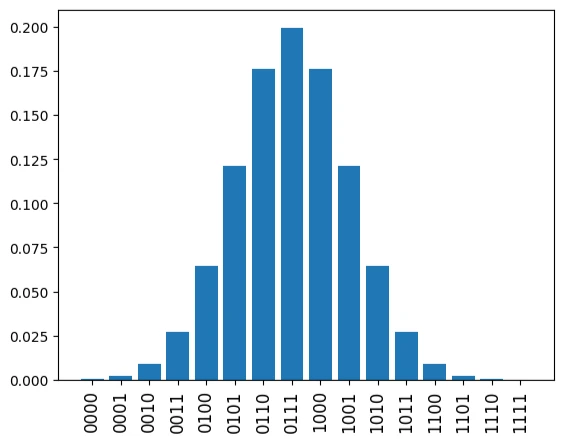
図で記載してみると以下の通りとなります。今回はこのデータを学習対象とします。

import matplotlib.pyplot as plt
%matplotlib inline
labels = [format(i, "b").zfill(n_qubits) for i in range(len(data))]
plt.bar(range(2**n_qubits), data)
plt.xticks(list(range(len(data))), labels, rotation="vertical", size=12)
plt.show()

量子機械学習アルゴリズムの実行

必要となるモジュールをインポートします。

from braket.devices import LocalSimulator
from braket.experimental.algorithms.quantum_circuit_born_machine import QCBM, mmd_loss

今回はローカルで計算を行うためデバイスをローカルデバイスとします。QCBMのようなハイブリッドアルゴリズムをAWS Managed Simulatorや、量子コンピュータで実行すると、高額な請求となる場合があります。この程度の回路であればローカルシミュレータでも十分計算できるので、ローカルシミュレータを上手く使いましょう。

device = LocalSimulator()

トレーニング対象のデータのビット数は4なので、量子ビット数はそれに対応して4と定義します。

n_qubits = 4

またQCBMではディープラーニングと似て層の数を定義できます。今回は層の数を4としましょう。これらのパラメータにより、QCBMのインスタンスを次のように作成できます。

n_layers = 4
qcbm = QCBM(device, n_qubits, n_layers, data)

これにより定義された量子回路を描画しましょう。層の数が4つ定義されています。

T  : │         0         │         1         │         2         │  3  │         4         │         5         │         6         │         7         │         8         │         9         │        10         │        11         │        12         │        13         │        14         │        15         │        16         │        17         │        18         │ 19  │ 20  │ Result Types  │
      ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐       ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐                                         ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐                                         ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐                                                     ┌─────────────┐ 
q0 : ─┤ Rx(theta_0_0_0) ├─┤ Rz(theta_0_0_1) ├─┤ Rx(theta_0_0_2) ├───●───┤ Rx(theta_1_0_0) ├─┤ Rz(theta_1_0_1) ├─┤ Rx(theta_1_0_2) ├──────────────────────────────●──────────┤ Rx(theta_2_0_0) ├─┤ Rz(theta_2_0_1) ├─┤ Rx(theta_2_0_2) ├──────────────────────────────●──────────┤ Rx(theta_3_0_0) ├─┤ Rz(theta_3_0_1) ├─┤ Rx(theta_3_0_2) ├──────────────────────────────●──────────────────────┤ Probability ├─
      └─────────────────┘ └─────────────────┘ └─────────────────┘   │   └─────────────────┘ └─────────────────┘ └─────────────────┘                              │          └─────────────────┘ └─────────────────┘ └─────────────────┘                              │          └─────────────────┘ └─────────────────┘ └─────────────────┘                              │                      └──────┬──────┘ 
      ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐ ┌─┴─┐                     ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐        ┌─┴─┐                            ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐        ┌─┴─┐                            ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐        ┌─┴─┐                    ┌──────┴──────┐ 
q1 : ─┤ Rx(theta_0_1_0) ├─┤ Rz(theta_0_1_1) ├─┤ Rx(theta_0_1_2) ├─┤ X ├──────────●──────────┤ Rx(theta_1_1_0) ├─┤ Rz(theta_1_1_1) ├─┤ Rx(theta_1_1_2) ├────────┤ X ├─────────────────●──────────┤ Rx(theta_2_1_0) ├─┤ Rz(theta_2_1_1) ├─┤ Rx(theta_2_1_2) ├────────┤ X ├─────────────────●──────────┤ Rx(theta_3_1_0) ├─┤ Rz(theta_3_1_1) ├─┤ Rx(theta_3_1_2) ├────────┤ X ├──────────●─────────┤ Probability ├─
      └─────────────────┘ └─────────────────┘ └─────────────────┘ └───┘          │          └─────────────────┘ └─────────────────┘ └─────────────────┘        └───┘                 │          └─────────────────┘ └─────────────────┘ └─────────────────┘        └───┘                 │          └─────────────────┘ └─────────────────┘ └─────────────────┘        └───┘          │         └──────┬──────┘ 
      ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐              ┌─┴─┐                            ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐        ┌─┴─┐                            ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐        ┌─┴─┐                            ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐ ┌─┴─┐       ┌──────┴──────┐ 
q2 : ─┤ Rx(theta_0_2_0) ├─┤ Rz(theta_0_2_1) ├─┤ Rx(theta_0_2_2) ├──────────────┤ X ├─────────────────●──────────┤ Rx(theta_1_2_0) ├─┤ Rz(theta_1_2_1) ├─┤ Rx(theta_1_2_2) ├────────┤ X ├─────────────────●──────────┤ Rx(theta_2_2_0) ├─┤ Rz(theta_2_2_1) ├─┤ Rx(theta_2_2_2) ├────────┤ X ├─────────────────●──────────┤ Rx(theta_3_2_0) ├─┤ Rz(theta_3_2_1) ├─┤ Rx(theta_3_2_2) ├─┤ X ├───●───┤ Probability ├─
      └─────────────────┘ └─────────────────┘ └─────────────────┘              └───┘                 │          └─────────────────┘ └─────────────────┘ └─────────────────┘        └───┘                 │          └─────────────────┘ └─────────────────┘ └─────────────────┘        └───┘                 │          └─────────────────┘ └─────────────────┘ └─────────────────┘ └───┘   │   └──────┬──────┘ 
      ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐                                  ┌─┴─┐        ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐                            ┌─┴─┐        ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐                            ┌─┴─┐        ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐       ┌─┴─┐ ┌──────┴──────┐ 
q3 : ─┤ Rx(theta_0_3_0) ├─┤ Rz(theta_0_3_1) ├─┤ Rx(theta_0_3_2) ├──────────────────────────────────┤ X ├────────┤ Rx(theta_1_3_0) ├─┤ Rz(theta_1_3_1) ├─┤ Rx(theta_1_3_2) ├────────────────────────────┤ X ├────────┤ Rx(theta_2_3_0) ├─┤ Rz(theta_2_3_1) ├─┤ Rx(theta_2_3_2) ├────────────────────────────┤ X ├────────┤ Rx(theta_3_3_0) ├─┤ Rz(theta_3_3_1) ├─┤ Rx(theta_3_3_2) ├───────┤ X ├─┤ Probability ├─
      └─────────────────┘ └─────────────────┘ └─────────────────┘                                  └───┘        └─────────────────┘ └─────────────────┘ └─────────────────┘                            └───┘        └─────────────────┘ └─────────────────┘ └─────────────────┘                            └───┘        └─────────────────┘ └─────────────────┘ └─────────────────┘       └───┘ └─────────────┘ 
T  : │         0         │         1         │         2         │  3  │         4         │         5         │         6         │         7         │         8         │         9         │        10         │        11         │        12         │        13         │        14         │        15         │        16         │        17         │        18         │ 19  │ 20  │ Result Types  │

Unassigned parameters: [theta_0_0_0, theta_0_0_1, theta_0_0_2, theta_0_1_0, theta_0_1_1, theta_0_1_2, theta_0_2_0, theta_0_2_1, theta_0_2_2, theta_0_3_0, theta_0_3_1, theta_0_3_2, theta_1_0_0, theta_1_0_1, theta_1_0_2, theta_1_1_0, theta_1_1_1, theta_1_1_2, theta_1_2_0, theta_1_2_1, theta_1_2_2, theta_1_3_0, theta_1_3_1, theta_1_3_2, theta_2_0_0, theta_2_0_1, theta_2_0_2, theta_2_1_0, theta_2_1_1, theta_2_1_2, theta_2_2_0, theta_2_2_1, theta_2_2_2, theta_2_3_0, theta_2_3_1, theta_2_3_2, theta_3_0_0, theta_3_0_1, theta_3_0_2, theta_3_1_0, theta_3_1_1, theta_3_1_2, theta_3_2_0, theta_3_2_1, theta_3_2_2, theta_3_3_0, theta_3_3_1, theta_3_3_2].

また学習の反復回数は10としましょう。

n_iterations = 10

この回路のゲートの数の通り、今回は3 * n_layers * n_qubitsのパラメータが必要となります。ではこのパラメータの初期値を定義します。

init_params = np.random.rand(3 * n_layers * n_qubits) * np.pi * 2

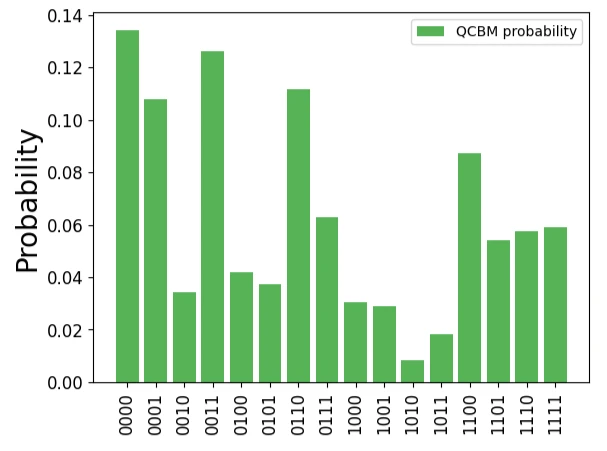
qcbm.get_probabilities(init_params)でこの初期状態の回路による確率分布が得られます。全く学習を進めていない状態ですので、以下の通りターゲットデータと全く異なる確率分布を出力することが確かめられます。

qcbm_probs = qcbm.get_probabilities(init_params)

plt.bar(range(2**n_qubits), qcbm_probs, label="QCBM probability", alpha=0.8, color="tab:green")
plt.xticks(list(range(len(data))), labels, rotation="vertical", size=12)
plt.yticks(size=12)
plt.ylabel("Probability", size=20)

plt.legend()
plt.show()

ではこのモデルで学習を進めましょう。勾配はqcbm.gradient(x)のように求められます。コードを見てみると勾配はこちらの論文の方法で求められているようです。また、損失関数はMMD Loss（Maximum Mean Discrepancy Loss）が用いられます。このため学習はscipyを用いて次のように進められます。

from scipy.optimize import minimize

history = []

def callback(x):
    loss = mmd_loss(qcbm.get_probabilities(x), data)
    history.append(loss)

result = minimize(
    lambda x: mmd_loss(qcbm.get_probabilities(x), data),
    x0=init_params,
    method="L-BFGS-B",
    jac=lambda x: qcbm.gradient(x),
    options={"maxiter": n_iterations},
    callback=callback,
)

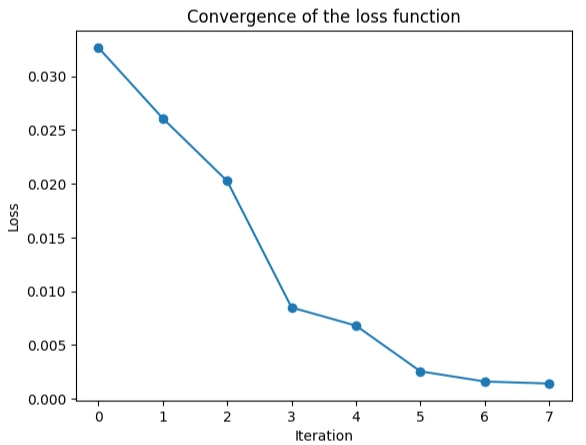
関数が収束する過程はこちらの通りです。

plt.plot(history, "-o")
plt.xlabel("Iteration")
plt.ylabel("Loss")
plt.title("Convergence of the loss function")

では学習後のパラメータで確率分布を習得し、ターゲットのデータと比較してみましょう。

qcbm_probs = qcbm.get_probabilities(result["x"])

plt.bar(range(2**n_qubits), data, label="target probability", alpha=1, color="tab:blue")
plt.bar(range(2**n_qubits), qcbm_probs, label="QCBM probability", alpha=0.8, color="tab:green")
plt.xticks(list(range(len(data))), labels, rotation="vertical", size=12)
plt.yticks(size=12)

plt.xlabel("Sample", size=20)
plt.ylabel("Probability", size=20)

plt.legend()
plt.show()

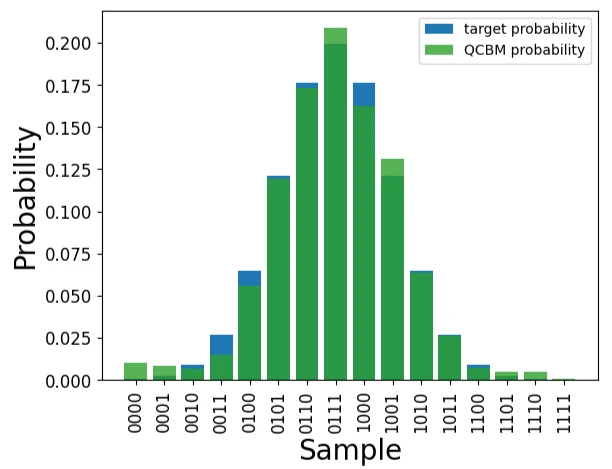
初期値のパラメータから学習が進んでいることが確認できました。

Amazon Braket学習コース

https://www.udemy.com/course/quantum-computing-on-aws-for-beginners-amazon-braket/?referralCode=F361C3FD774489A1B5B8

Qiskit試験対策問題集

qiskitについての資格試験をIBMが提供しています。

この資格を取得することでqiskitや量子プログラミングに関する知識を証明することが可能です。こちらの資格取得を目指される方のため、Udemyというサイト上にて日本語版、英語版で問題集を作りました！解説もなるべくわかりやすく作成いたしましたので、是非是非ご活用ください。

英語版問題集

https://www.udemy.com/course/ibm-certified-quantum-computation-qiskit-practice-exams/?referralCode=3B3263DF800E05439AD2

日本語版問題集

https://www.udemy.com/course/ibm-certified-quantum-computation-qiskit-jp/?referralCode=7D18ADD30A495E12120B