AWSのAmazon Braketでショアのアルゴリズム
これまでの記事では以下の内容を学びました：
- 量子フーリエ変換を具体例で理解
- Qiskit 2.0で逆量子フーリエ変換
- Amazon Braket SDKで逆量子フーリエ変換
- Qiskit 2.0で量子位相推定
- Amazon Braket SDKで量子位相推定
これらを踏まえてRSA暗号や、ビットコインのトランザクションで利用されるECDSA暗号を破ると言われている量子アルゴリズムであるショアのアルゴリズムについて学びます。
Amazon Braket学習コース
この記事で登場する、量子ゲートや量子回路など、量子コンピュータの基本的な知識や、Amazon Braketの使い方についてはこちらのコースで効率的に学べます。
量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう！
Qiskit試験対策問題集
qiskitについての資格試験をIBMが提供しています。
この資格を取得することでqiskitや量子プログラミングに関する知識を証明することが可能です。 こちらの資格取得を目指される方のため、Udemyというサイト上にて日本語版、英語版で問題集を作りました！解説もなるべくわかりやすく作成いたしましたので、是非是非ご活用ください。
英語版問題集
日本語版問題集
ショアのアルゴリズム
量子コンピューターで十分な数の量子ビットが扱えるようになった場合、ショアのアルゴリズムでRSA暗号や、ECDSA暗号が破られる危険性があると言われています。
例えばRSA暗号は大きな数の素因数分解が困難であることを利用した暗号方式ですが、今回はショアのアルゴリズムで素因数分解を行う例についてみていきましょう。
このアルゴリズムを用いて整数$N$の素因数分解を行う際の流れは以下の通りです。
$1 < a < N$ かつ$ N$との最大公約数が $1$ となる$a$を選ぶ
$\downarrow$
$a^x\bmod\ N$ という関数の周期 $r$を見つける
$\downarrow$
$a^{\frac{r}{2}} \pm 1$の最大公約数からNの素因数を求める
ここで"$a^x\bmod\ N$ という関数の周期 $r$を見つける"と記載されていますが、具体例を見ていきましょう。
例として$N=39$を素因数分解する際に、$a=5$を選んだ場合について考えます。$a^x\bmod\ N\ =\ 5^x\bmod\ 39$のグラフは$x$を横軸とすると次の通りとなります。
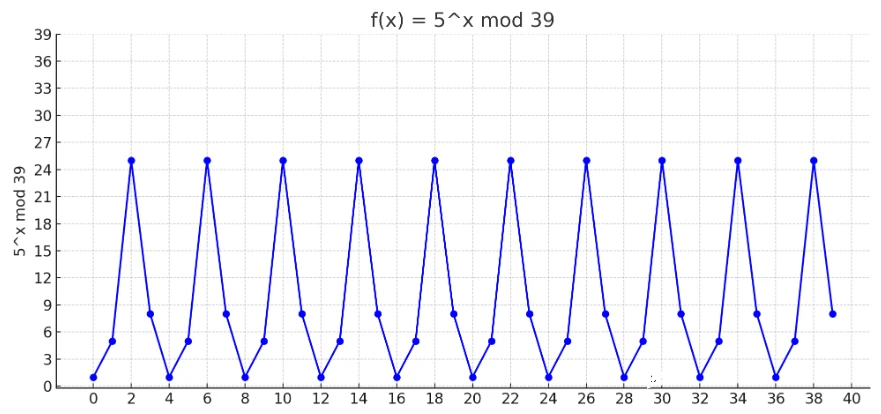
y軸の値を書き出すと以下の通りで、4回の変化を通じて元の値に戻る周期関数であることがわかります。
$$ 1 \rightarrow 5 \rightarrow 25 \rightarrow 8 \rightarrow 1 \rightarrow 5 \rightarrow 25 \rightarrow 8 \tag{1} $$
この周期が位数$r$となり、この場合は4回で元の値に戻るため、$r=4$を持つことがわかります。 ショアのアルゴリズムでは、この$r$を量子コンピュータで計算することで高速に因数分解を行います。
ここでショアのアルゴリズムの実装については$a^x\bmod\ N$の関数を量子回路に直接定義し利用する、汎用性があり実装が複雑な方法か、特定の $a, N$のペアに対しての$a^x\bmod\ N$の変化の結果から演算子を定義し利用する、より簡単な実装方法が存在します。
今回は特定の$a, N$のペアに対して実装する、より簡単な方法について説明します。
まずは下準備です。 $a^x\bmod\ N$という周期関数の変化をもたらす演算子は次のように表現できます。
$$ U |y\rangle = |a y\bmod\ N\rangle \tag{2} $$
これについて例を見て確認しましょう。例として既に登場した$N=39$で$a=5$のケースで考えます。この場合、式は以下の通りとなります。
$$ U |y\rangle = |5 y\bmod\ 39\rangle $$
$y = 1$を代入した場合以下の通りとなります。
$$ U |1\rangle = |5 \cdot 1\bmod\ 39\rangle = |5\rangle $$
この結果を再び$y$に代入すると以下の通りとなります。
$$ U |5\rangle = |5 \cdot 5\bmod\ 39\rangle = |25\rangle $$
再度この結果を代入しましょう。
$$ U |25\rangle = |5 \cdot 25\bmod\ 39\rangle = |8\rangle $$
再び代入します。
$$ U |8\rangle = |5 \cdot 8\bmod\ 39\rangle = |1\rangle $$
結果が $1$に戻りました！
確かにこの演算子により、(1)の変化を再現できており、この演算子を使えば位数rが求められるかもしれないと期待できます。(すでにこの時点で位数rの値はわかっているかもしれませんが、量子回路から回答を導くことが目的となるため、わからないふりをしておきます。)
ここで、(2)を満たす$U$の固有値は、固有状態を$|u_s\rangle$とした時、以下となることが知られています。
$$ U|u_s\rangle =\ e^{\frac{2\pi i s}{r}}|u_s\rangle $$
これは、量子位相推定アルゴリズムにより解を導ける形ですね！ さらにこの演算子の固有状態は以下で表せます。
$$
|u_s\rangle =
\frac{1}{\sqrt{r}}
\sum_{k=0}^{r-1}
e^{-\frac{2\pi i s k}{r}}
\bigl|a^{k}\bmod N\bigr\rangle
\quad (s = 0,1,\dots,r-1)
$$
この固有状態について、$r=4$などの値を代入し、実際に足し合わせてみてもわかりますが、全ての$s$について$|u_s\rangle$を足し合わせると $|1\rangle$となります。
$$ |1\rangle = \frac{1}{\sqrt{r}} ( |u_0\rangle + |u_1\rangle +….. |u_{r-1}\rangle ) $$
量子位相推定アルゴリズムでは、固有状態を量子ビットで定義することで、その固有状態に対する固有値を求めることができたのでした。 これらの性質より、固有状態を定義するビットを$|1\rangle$と設定し量子位相推定を実行することで、以下のような固有値の重ね合わせ$|\psi\rangle$が得られます。ここで、$n$は読み出しレジスタの量子ビット数です。
$$ |\psi\rangle = \frac{1}{\sqrt{r}} ( |2^n\cdot\frac{0}{r}\rangle + |2^n\cdot\frac{1}{r}\rangle +… + |2^n\cdot\frac{r - 1}{r}\rangle ) $$
この中に、rの情報も含まれているので$|\psi\rangle$を観測すれば結果からrを推定することができます。
この方法の流れをまとめると以下の通りとなります。
対象の$a, N$について、$U |y\rangle = |a y\bmod\ N\rangle$の変化をもたらす $U$を定義する
$\downarrow$
固有状態の重ね合わせである$|1\rangle$と $U$について量子位相推定を行う
$\downarrow$
観測結果から $r$を推定する
実際に試してみましょう！
Amazon Braket SDKでの実装
せっかくなのでより大きい値である$N=341$を素因数分解の対象としましょう。 また、$a=32$と今回設定し、実装します。 まずは$a=32, N=341$について、$U |y\rangle = |a y\bmod\ N\rangle$の変化をもたらす $U$を定義します。$y=1$を代入すると次のような結果が得られます。 $$ U |1\rangle = |32 \cdot 1\bmod\ 341\rangle = |32\rangle $$ この結果を再度$y$に代入します。 $$ U |32\rangle = |32 \cdot 32\bmod\ 341\rangle = |1\rangle $$ $|1\rangle$に戻りました！よって変化としては以下の通り記載できます。
$$ |1\rangle \rightarrow |32\rangle \rightarrow |1\rangle \rightarrow |32\rangle \rightarrow |1\rangle \tag{3} $$ この変化をもたらす $U$は固有状態レジスタの6番目の量子ビットにXゲートを適用することで定義できます。 ではこの $U$と、$|1\rangle$について量子位相推定アルゴリズムを実施しましょう。まずはこちらで紹介されているコードの通り、読み出しレジスタにHゲートを適用するところまで記載します。
from braket.circuits import Circuit
from braket.devices import LocalSimulator
from braket.experimental.algorithms.quantum_fourier_transform import (
quantum_fourier_transform as qft_module
)
n_readout_qubits = 3
circ = Circuit()
for qubit in list(range(n_readout_qubits)):
circ.h(qubit)
この後、$|1\rangle$を次のように定義します。
circ.x(n_readout_qubits)
では、(3)の変化をもたらす制御$U$ゲートを、量子位相推定アルゴリズムの規則で適用します。
n_eigenstate_qubits = 6
for ctl_bit in list(range(n_readout_qubits)):
for i in list(range(2**(ctl_bit))):
circ.cnot(ctl_bit, n_readout_qubits + n_eigenstate_qubits - 1)
最後に逆量子フーリエ変換です。
circ.swap(0,n_readout_qubits - 1)
circ.iqft(range(n_readout_qubits))
circ.measure([0, 1, 2])
device = LocalSimulator()
result = device.run(circ, shots=1000).result()
counts = result.measurement_counts
print(counts)
# Output
# Counter({'000': 501, '100': 499})
このような結果からrを推定するコードについてはこちらのget_factors_from_results()が参考となります。
今回は結果から、$r=2$が推定できます。
こちらの$r$を用いれば、$a^{\frac{r}{2}} + 1 = 33$、$a^{\frac{r}{2}} - 1 = 31$と求まります。
そしてこの2つの数と341との最大公約数は以下の通りです。
$$ \begin{align} gcd(33, 341) = 11 \\ gcd(31, 341) = 31 \end{align} $$ 無事に341の素因数が11、31と求まりました！
Amazon Braket学習コース
この記事で登場する、量子ゲートや量子回路など、量子コンピュータの基本的な知識や、Amazon Braketの使い方についてはこちらのコースで効率的に学べます。
量子コンピュータやAWSの知識が無い方でも学び始められ、最終的には量子機械学習についても学べます。 こちらも利用し、量子技術のスキルを身につけましょう！
Qiskit試験対策問題集
qiskitについての資格試験をIBMが提供しています。
この資格を取得することでqiskitや量子プログラミングに関する知識を証明することが可能です。 こちらの資格取得を目指される方のため、Udemyというサイト上にて日本語版、英語版で問題集を作りました！解説もなるべくわかりやすく作成いたしましたので、是非是非ご活用ください。