Inverse Quantum Fourier Transform on AWS Amazon Braket
In the previous article, we implemented the Inverse Quantum Fourier Transform using Qiskit 2.0 and verify that the original quantum state can be correctly identified.
In this article, we will implement the Inverse Quantum Fourier Transform using Amazon Braket SDK.
Amazon Braket Learning Course
You can efficiently learn the basic knowledge of quantum computing—including quantum gates and quantum circuits introduced in this article—as well as how to use Amazon Braket through this course.
This course is designed for those with no prior knowledge of quantum computing or AWS, and by the end, you’ll even be able to learn about quantum machine learning. Take advantage of this opportunity to build your skills in quantum technologies!
The Inverse Quantum Fourier Transform using Amazon Braket SDK
In the previous article, we explained that if a 2-qubit quantum state existed in either state $\psi_1 = \frac{1}{2} \left( \ket{00} + i\ket{01} - \ket{10} - i\ket{11} \right)$ or $\psi_2 = \frac{1}{2} \left( \ket{00} - \ket{01} + \ket{10} - \ket{11} \right)$, it is possible to determine which state it is by applying the Inverse Quantum Fourier Transform.
Also, in this article, we implemented the Inverse Quantum Fourier Transform using Qiskit 2.0.
This time, we will perform the Inverse Quantum Fourier Transform using Amazon Braket SDK and verify that the original quantum state can be correctly identified.
Firstly, let’s import the necessary functions.
from braket.circuits import Circuit
from braket.devices import LocalSimulator
from braket.experimental.algorithms.quantum_fourier_transform import (
quantum_fourier_transform as qft_module
)
We define Quancum Cruicuit.
n_qubits = 2
circ = Circuit()
As in the previous case, let’s define $\psi_2$ in advance, and then perform the inverse Quantum Fourier Transform.
Here, the inverse Quantum Fourier Transform circuits from the previous Qiskit implementation and the current one using the Amazon Braket SDK’s algorithm library are shown below, and they are reversed with respect to each other.
-
Quantum Circuit in the previous Qiskit implementation
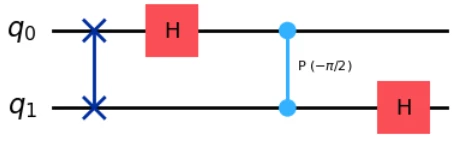
-
The current one using the Amazon Braket SDK’s algorithm library
T : │ 0 │ 1 │ 2 │ 3 │
┌──────────────┐ ┌───┐
q0 : ────x───────────┤ PHASE(-1.57) ├─┤ H ├─
│ └──────┬───────┘ └───┘
│ ┌───┐ │
q1 : ────x─────┤ H ├────────●───────────────
└───┘
T : │ 0 │ 1 │ 2 │ 3 │
When taking this order into account-that is, when preparing $\psi_2$ to be compatible with the Quantum Fourier Transform in the Amazon Braket SDK-the following circuit is required.
circ.h(0)
circ.x(1)
circ.h(1)
This is illustrated in the diagram below.
T : │ 0 │ 1 │
┌───┐
q0 : ─┤ H ├───────
└───┘
┌───┐ ┌───┐
q1 : ─┤ X ├─┤ H ├─
└───┘ └───┘
T : │ 0 │ 1 │
Now, let’s execute the Quantum Fourier Transform.
circ.iqft(range(n_qubits))
device = LocalSimulator()
result = device.run(circ, shots=1000).result()
counts = result.measurement_counts
print(counts)
As shown below, the result observes state $\ket{10}$, indicating that state $\psi_2$ was originally generated. Similarly, if you generate state $\psi_1$ and then apply the Inverse Quantum Fourier Transform, you will observe state$\ket{01}$. Give it a try when you have a moment.
Counter({'10': 1000})
Amazon Braket Learning Course
You can efficiently learn the basic knowledge of quantum computing—including quantum gates and quantum circuits introduced in this article—as well as how to use Amazon Braket through this course.
This course is designed for those with no prior knowledge of quantum computing or AWS, and by the end, you’ll even be able to learn about quantum machine learning. Take advantage of this opportunity to build your skills in quantum technologies!
